We're using a Jupyter Notebook with Python (programming language) and Pandas (data science framework) to classify British Columbia's BioGeoClimatic zones by the Koppen-Geiger global classification system.
This should help understand which global species may be interested in invading specific areas of BC.
We'll start by importing Pandas (to be honest, we're barely using it; we could just as well use the Python CSV library for everything we're doing here, but in the future some of the power of Pandas might come in handy).
import pandas as pd
Let's open the BioGeoClimatic zone data as a Pandas DataFrame object. The data has been rescued from Microsoft Access via a table export and is in the working directory as a comma-delimited text file called BGC_Units.txt.
df = pd.read_csv('BGC_Units.txt')
# Let's take a look at it.
df
| ID | BGC | period | Var | Tmax01 | Tmax02 | Tmax03 | Tmax04 | Tmax05 | Tmax06 | ... | bFFP | eFFP | FFP | PAS | EMT | EXT | Eref | CMD | MAR | RH | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | BAFAun | 1961-1990 | 5% | -17.43 | -11.65 | -8.10 | -2.50 | 3.67 | 7.65 | ... | 168.31 | 214.95 | 29.37 | 782.45 | -44.43 | 24.31 | 218.71 | 4.05 | 11.23 | 64.42 |
| 1 | 2 | BAFAun | 1961-1990 | 95% | -1.73 | -0.82 | -0.81 | 2.75 | 7.55 | 12.74 | ... | 190.88 | 241.60 | 67.94 | 1250.45 | -44.43 | 24.31 | 291.38 | 74.26 | 12.05 | 69.39 |
| 2 | 3 | BAFAun | 1961-1990 | max | -0.25 | 0.55 | -0.29 | 3.65 | 8.06 | 13.82 | ... | 193.40 | 248.78 | 78.54 | 1346.27 | -44.43 | 24.31 | 306.78 | 93.98 | 12.16 | 69.97 |
| 3 | 4 | BAFAun | 1961-1990 | mean | -8.86 | -6.50 | -4.46 | 0.18 | 5.57 | 9.68 | ... | 180.59 | 228.16 | 47.58 | 1005.53 | -44.43 | 24.31 | 256.92 | 33.79 | 11.67 | 67.00 |
| 4 | 5 | BAFAun | 1961-1990 | min | -20.81 | -15.83 | -9.04 | -3.68 | 3.17 | 7.34 | ... | 154.99 | 212.09 | 25.43 | 706.22 | -44.43 | 24.31 | 206.75 | 1.78 | 11.15 | 63.32 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 11867 | 11868 | SWB vks | 1990-2014 | max | -0.52 | -0.41 | 0.80 | 6.69 | 11.86 | 14.93 | ... | 191.90 | 262.15 | 98.39 | 3003.38 | -40.00 | 26.15 | 362.39 | 34.00 | 11.23 | 73.92 |
| 11868 | 11869 | SWB vks | 1990-2014 | mean | -6.76 | -4.31 | -1.81 | 4.01 | 9.29 | 12.85 | ... | 171.90 | 246.25 | 74.34 | 2203.05 | -40.00 | 26.15 | 311.08 | 7.80 | -1590.87 | 71.58 |
| 11869 | 11870 | SWB vks | 1990-2014 | min | -15.25 | -9.29 | -6.02 | 0.45 | 6.22 | 10.61 | ... | 155.80 | 217.42 | 37.28 | 1342.06 | -40.00 | 26.15 | 269.60 | 0.00 | -9999.00 | 67.80 |
| 11870 | 11871 | SWB vks | 1990-2014 | st.dev.Ann | 3.04 | 2.61 | 1.86 | 1.57 | 1.54 | 1.14 | ... | 9.93 | 10.33 | 16.40 | 421.88 | 0.00 | 0.00 | 25.48 | 10.52 | 3745.27 | 1.71 |
| 11871 | 11872 | SWB vks | 1990-2014 | st.dev.Geo | 1.52 | 1.39 | 1.20 | 0.90 | 0.83 | 0.84 | ... | 7.78 | 5.47 | 13.04 | 603.21 | 1.73 | 0.66 | 20.55 | 5.41 | 0.72 | 3.14 |
11872 rows × 251 columns
The explanations (helpstrings) of the cryptic column names are in a CSV file called tblTasksFields.csv (which needed a bit of extra massaging after rescuing from MSAccess to remove non-compliant Unicode degree symbols).
hs = pd.read_csv('tblTasksFields.csv')
hs
| TaskFieldD | FieldName | FieldOrder | DisplayOrder | Label1 | Label2 | Label3 | Flag | F9 | Group | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -2143629518 | DD5_04 | 70 | 150.0 | Degree-days above 5 deg C | April (mm) | growing degree-days | 0 | 0 | Monthly |
| 1 | -2113721533 | Tmax09 | 27 | 95.0 | Temperature max | September ( deg C) | NaN | 0 | 0 | Monthly |
| 2 | -2084351942 | RH08 | 242 | 238.0 | Relative humidity | August | NaN | 0 | 0 | Monthly |
| 3 | -2061850604 | DD_18_06 | 84 | 164.0 | Degree-days below 18 deg C | June (mm) | heating degree-days | 0 | 0 | Monthly |
| 4 | -2041423190 | NFFD08 | 110 | 190.0 | the number of frost-free days | August | NaN | 0 | 0 | Monthly |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 242 | 2062216706 | Rad12 | 230 | 134.0 | Radiation | December(MJ m-2d-1) | NaN | 0 | 0 | Monthly |
| 243 | 2069203954 | Eref08 | 134 | 214.0 | Hargreaves reference evaporation | August | NaN | 0 | 0 | Monthly |
| 244 | 2075199413 | PPT07 | 49 | 117.0 | Precipitation | July (mm) | NaN | 0 | 0 | Monthly |
| 245 | 2090761322 | MCMT | 6 | 3.0 | Mean coldest month( deg C) | NaN | NaN | 1 | 0 | Monthly |
| 246 | 2123389953 | DD_0_03 | 57 | 137.0 | Degree-days below 0 deg C | March (mm) | chilling degree-days | 0 | 0 | Monthly |
247 rows × 10 columns
Let's make a dictionary with the column names as the keys and the description helpstrings as the values. We've manually identified column 2 as containing the zone/subzone/variant id string and column 5 as containing the explanatory helpstring.
colnames = {}
for item in hs.itertuples():
colnames[item[2]] = item[5]
Let's look at all of the column headers, the type of each column (Pandas infers a datatype for an entire column based on the values it finds in them), and the explanatory helpstrings.
cols = [[x[0], x[1], colnames.get(x[0])]
for x in zip(df.columns, df.dtypes)]
# Print first 25 columns to get a sense of the schema
for name in cols[:25]:
print(name)
['ID', dtype('int64'), None]
['BGC', dtype('O'), None]
['period', dtype('O'), None]
['Var', dtype('O'), None]
['Tmax01', dtype('float64'), 'Temperature max']
['Tmax02', dtype('float64'), 'Temperature max']
['Tmax03', dtype('float64'), 'Temperature max']
['Tmax04', dtype('float64'), 'Temperature max']
['Tmax05', dtype('float64'), 'Temperature max']
['Tmax06', dtype('float64'), 'Temperature max']
['Tmax07', dtype('float64'), 'Temperature max']
['Tmax08', dtype('float64'), 'Temperature max']
['Tmax09', dtype('float64'), 'Temperature max']
['Tmax10', dtype('float64'), 'Temperature max']
['Tmax11', dtype('float64'), 'Temperature max']
['Tmax12', dtype('float64'), 'Temperature max']
['Tmin01', dtype('float64'), 'Temperature min']
['Tmin02', dtype('float64'), 'Temperature min']
['Tmin03', dtype('float64'), 'Temperature min']
['Tmin04', dtype('float64'), 'Temperature min']
['Tmin05', dtype('float64'), 'Temperature min']
['Tmin06', dtype('float64'), 'Temperature min']
['Tmin07', dtype('float64'), 'Temperature min']
['Tmin08', dtype('float64'), 'Temperature min']
['Tmin09', dtype('float64'), 'Temperature min']
Ok, the first column is an incrementing ID, the following three columns are objects (well, strings). The remaining columns are all numbers, mostly floating-point decimals with a few integers here and there. Note that many seem to consist of a string like Tmax followed by a number between 01 and 12; these represent months.
Let's grab the three string columns and see how many unique values they contain, and what they are. From the previous cell's output, we know that the first is a zone/subzone/variant ID string, the second a range from a start to end year, and the third describes the statistical operation that's generated the actual values in the row.
A Python set will allow us to look at only the unique values, so we can see all of the different zones, date ranges, and statistical operations that the values come from.
dateranges = set()
bgczones = set()
vardefs = set()
for row in df.itertuples():
bgczones.add(row[2])
dateranges.add(row[3])
vardefs.add(row[4])
Let's look at all of the unique date ranges, statistical outputs, and zone/subzone/variant identifiers in the data:
print(f'There are {len(dateranges)} unique date '\
f'ranges:\n{dateranges}')
print(f'\nThere are {len(vardefs)} unique statistical '\
f'operations the values come from: \n{vardefs}')
print(f'\nThere are {len(bgczones)} unique zone/subzone'\
f'/variants: \n{bgczones}')
There are 8 unique date ranges:
{'1901-1960', '1961-1990', '1945-1976', '1901-1990', '1901-2014', '1977-1998', '1971-2000', '1990-2014'}
There are 7 unique statistical operations the values come from:
{'5%', 'mean', 'st.dev.Ann', 'min', 'st.dev.Geo', 'max', '95%'}
There are 212 unique zone/subzone/variants:
{'ESSFmv 2', 'ESSFmv 1', 'BG xh 1', 'ICH vc', 'BAFAun', 'MS dc 1', 'SBPSmk', 'ESSFmmp', 'ESSFvcw', 'ICH mk 4', 'ESSFvcp', 'SBS dh 1', 'ESSFvm', 'ICH mw 3', 'IDF ww', 'ICH mc 2', 'SBS mc 1', 'ESSFdk 1', 'IDF dk 4', 'CWH ds 2', 'BWBSmk', 'CMA un', 'ICH mm', 'SBS dk', 'IDF dm 1', 'IDF dw', 'MS xv', 'IDF xx 2', 'IMA unp', 'ICH mk 3', 'SBS wk 1', 'ESSFmv 3', 'CWH mm 2', 'ESSFdv 1', 'ICH wk 4', 'ICH mw 1', 'PP xh 2', 'ESSFdvp', 'BG xh 2', 'MS dk', 'ESSFmkp', 'MH un', 'SBS mk 2', 'ESSFwk 1', 'ESSFmww', 'ICH mk 1', 'IDF dk 5', 'IDF mw 2', 'IDF dk 3', 'IMA un', 'BWBSwk 2', 'SBS dw 1', 'SBS dw 3', 'ESSFwm 3', 'ESSFdkw', 'ESSFdcp', 'ESSFwm 4', 'SBS mm', 'MS xk 1', 'IDF xc', 'CMA unp', 'ESSFxv 2', 'IDF dc', 'ICH mk 2', 'ESSFmm 1', 'ESSFdc 3', 'ESSFwc 2', 'ESSFdkp', 'ESSFxc 1', 'SBPSmc', 'ESSFmh', 'ESSFmvp', 'CDF mm', 'CWH vm 1', 'MS dm 2', 'MS dv', 'MS dw', 'IDF xh 1', 'SBS wk 2', 'ESSFwm 2', 'ESSFxvw', 'CWH wh 2', 'IDF xm', 'ESSFwh 3', 'SWB uns', 'MH mm 2', 'ICH wk 1', 'CWH wm', 'IDF dm 2', 'BWBSmw', 'SWB mks', 'SBPSdc', 'ICH dk', 'ESSFwc 4', 'ESSFwh 1', 'ESSFxc 2', 'IDF dh', 'ICH mc 1', 'ESSFmm 2', 'SBS dh 2', 'SBS un', 'CWH ws 2', 'CWH vm 2', 'ESSFmw 2', 'IDF mw 1', 'CWH mm 1', 'CWH xm 2', 'ESSFmk', 'ICH wk 3', 'ESSFvc', 'ESSFdc 2', 'IDF xk', 'SBPSxc', 'ESSFwv', 'ESSFdv 2', 'CWH ms 1', 'ICH xw', 'CWH vh 3', 'ICH dw 1', 'CWH vm 1N', 'ICH mw 5', 'ICH vk 1', 'ESSFun', 'MS dc 3', 'ICH wk 2', 'SBS mc 3', 'BAFAunp', 'CWH wh 1', 'ESSFmw', 'CWH dm', 'BWBSdk', 'MS dm 3', 'CWH ms 2', 'CWH vh 1', 'ICH mw 2', 'MS dm 1', 'ESSFmwp', 'MH unp', 'MH mmp', 'BG xw 2', 'ESSFwcw', 'ESSFmc', 'IDF xx 1', 'SBS mk 1', 'ESSFxv 1', 'MH mm 1', 'ESSFwm 1', 'ESSFmv 4', 'ESSFdk 2', 'BG xh 3', 'ESSFmmw', 'ICH mw 4', 'ICH mk 5', 'PP xh 1', 'ESSFxvp', 'IDF dk 2', 'ESSFwmp', 'ESSFwk 2', 'ESSFwc 3', 'SBS wk 3', 'ESSFdh 2', 'ICH mw 6', 'SBS dw 2', 'MH wh', 'SBS mw', 'SWB vk', 'ESSFdcw', 'ESSFdc 1', 'ESSFwcp', 'ICH wc', 'IDF xh 2', 'PP xw', 'MH whp', 'CWH vh 2', 'ESSFwvp', 'ICH dm', 'SWB mk', 'BWBSvk', 'ESSFxc 3', 'ESSFdh 1', 'SWB vks', 'ESSFxcw', 'SBS mh', 'BWBSwk 1', 'ESSFunp', 'CWH un', 'MH wh 1', 'CMA wh', 'IDF ww 1', 'CWH ds 1', 'ESSFmw 1', 'ESSFwmw', 'ESSFwh 2', 'SBS vk', 'SBS mc 2', 'MS un', 'ICH dw 3', 'MS dc 2', 'MS xk 3', 'ICH vk 2', 'MS xk 2', 'IDF dk 1', 'ESSFxcp', 'BWBSwk 3', 'CWH xm 1', 'ESSFdvw', 'ESSFmcp', 'BG xw 1', 'ESSFvk', 'SWB un', 'CWH ws 1', 'IDF xw'}
Right! For the moment, we only want to consider the date range from 1961 to 1990, since we're comparing our results to previous work that used that range.
Furthermore, we only want to use the mean values to key out the Koppen-Geiger classes of the zone/subzone/variants. Someone smarter than us may later wish to do a more sophisticated classification, but not today.
So we're only going to using a small subset of the data to classify the zone/subzone/variants. Let's create that subset now with a filter.
# create a filtered DataFrame (call it fdf)
fdf = df[(df['period']=='1961-1990') & (df['Var']=='mean')]
fdf
| ID | BGC | period | Var | Tmax01 | Tmax02 | Tmax03 | Tmax04 | Tmax05 | Tmax06 | ... | bFFP | eFFP | FFP | PAS | EMT | EXT | Eref | CMD | MAR | RH | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 4 | BAFAun | 1961-1990 | mean | -8.86 | -6.50 | -4.46 | 0.18 | 5.57 | 9.68 | ... | 180.59 | 228.16 | 47.58 | 1005.53 | -44.43 | 24.31 | 256.92 | 33.79 | 11.67 | 67.00 |
| 87 | 88 | BAFAunp | 1961-1990 | mean | -4.83 | -1.79 | 0.40 | 3.34 | 8.12 | 11.64 | ... | 182.28 | 238.45 | 56.16 | 1044.44 | -41.48 | 27.29 | 356.45 | 103.08 | 12.94 | 63.66 |
| 143 | 144 | BG xh 1 | 1961-1990 | mean | 0.04 | 4.46 | 10.50 | 16.06 | 21.03 | 25.30 | ... | 113.32 | 287.28 | 173.96 | 46.62 | -29.82 | 39.23 | 800.85 | 589.01 | -32.28 | 64.80 |
| 199 | 200 | BG xh 2 | 1961-1990 | mean | -1.89 | 2.95 | 9.33 | 15.24 | 20.21 | 24.47 | ... | 123.88 | 278.51 | 154.61 | 65.00 | -33.37 | 37.53 | 751.19 | 564.76 | 11.21 | 62.35 |
| 255 | 256 | BG xh 3 | 1961-1990 | mean | -2.78 | 2.55 | 8.77 | 14.54 | 19.48 | 23.69 | ... | 131.22 | 273.63 | 142.39 | 74.45 | -34.92 | 37.26 | 726.20 | 518.15 | 11.12 | 60.91 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 11623 | 11624 | SWB mks | 1961-1990 | mean | -8.69 | -5.73 | -3.41 | 2.53 | 7.96 | 12.13 | ... | 180.82 | 233.45 | 52.63 | 495.86 | -44.37 | 26.15 | 307.56 | 46.95 | 11.01 | 65.32 |
| 11679 | 11680 | SWB un | 1961-1990 | mean | -10.73 | -6.33 | -2.07 | 3.68 | 9.38 | 14.21 | ... | 176.09 | 235.97 | 59.87 | 375.10 | -45.50 | 28.35 | 342.42 | 106.42 | 10.15 | 61.44 |
| 11735 | 11736 | SWB uns | 1961-1990 | mean | -10.08 | -6.26 | -3.08 | 2.10 | 7.91 | 12.57 | ... | 178.06 | 232.03 | 53.96 | 455.28 | -45.51 | 26.83 | 306.25 | 76.70 | 10.34 | 62.26 |
| 11791 | 11792 | SWB vk | 1961-1990 | mean | -6.95 | -3.82 | -0.41 | 4.32 | 9.35 | 13.08 | ... | 161.33 | 251.51 | 90.16 | 1394.19 | -37.62 | 27.25 | 328.85 | 12.43 | -89.72 | 72.52 |
| 11847 | 11848 | SWB vks | 1961-1990 | mean | -8.63 | -5.42 | -2.11 | 2.80 | 7.92 | 11.72 | ... | 174.74 | 240.86 | 66.13 | 2292.16 | -40.00 | 26.15 | 299.63 | 6.66 | 10.82 | 71.04 |
212 rows × 251 columns
Nice! Not only is this a much smaller dataset, we can see that it has the same number of rows as there are unique zone/subzone/variants. That's a good sanity check on the filter as well as a bit of reassurance regarding the quality of the dataset.
Let's build a function that accepts a row from the dataset as input, and returns a Koppen-Geiger class string if it matches the parameters, or None if not.
First we'll need some helper functions!
Most of the Koppen-Geiger criteria involve finding minimum and maximum temperature and/or precipitation values across multiple months. For example, the average temperature is found in the dataset in columns with headers labelled Tave01 Tave02...Tave12 for January through December. So we'll create a helper function (twelvemonther) to generate those column names so we can use them as keys to extract the appropriate series.
Additionally, the algorithm often wants to compare winter and/or summer maxima and minima (with summer in the Northern Hemisphere defined as April-September and winter as October-March. So we'll create two more helper functions (summer and winter) to generate those column names.
def twelvemonther(s):
"""Creates a list with 01 to 12 appended to a given string"""
return [f'{s}{str(x + 1).zfill(2)}' for x in range(12)]
def summer(s):
"""Creates a list with 04 to 09 appended to a given string
because summer is defined as April-September in K-G."""
return [f'{s}{str(x + 1).zfill(2)}' for x in range(3,9)]
def winter(s):
"""Creates a list with 01 to 03 and 10 to 12 appended to a given
string because winter is defined as October-March in K-G."""
jan_mar = [f'{s}{str(x + 1).zfill(2)}' for x in range(3)]
oct_dec = [f'{s}{str(x + 1).zfill(2)}' for x in range(9,12)]
return jan_mar + oct_dec
Now we'll create some functions for each of the three letters in the Koppen-Geiger system. The rug that ties the room together will come after we sort out the individual letters based on the rules in the key algorithm (which we've copied into comments in the code).
def first(m, y):
"""returns first letter of the Koppen-Geiger classification"""
# A
# Temperature of coolest month 18 degrees Celsius or higher
if min(m['tave']) >= 18:
return 'A'
# B2
# **(why is it B2? Where is B1? Or plain old B?)**
# 70% or more of annual precipitation falls in the summer half
# of the year and r less than 20t + 280, or 70% or more of annual
# precipitation falls in the winter half of the year and r less
# than 20t, or neither half of the year has 70% or more of annual
# precipitation and r less than 20t + 1403"""
# C
# Temperature of warmest month greater than or equal to
# 10 degrees Celsius, and temperature of coldest month
# less than 18 degrees Celsius but greater than –3 degrees
# Celsius"""
if max(m['tave']) >= 10 and -3 < min(m['tave']) < 19:
return 'C'
# D
# Temperature of warmest month greater than or equal to
# 10 degrees Celsius, and temperature of coldest month
# –3 degrees Celsius or lower
if max(m['tave']) >= 10 and min(m['tave']) < -3:
return 'D'
# E
# Temperature of warmest month less than 10 degrees Celsius
if min(m['tave']) < 10:
return 'E'
# A through E all failed to return anything
return ''
def c_d_second(m, y):
"""returns second letter of the Koppen-Geiger classification
in the cases that the first letter is C or D"""
# s
# Precipitation in driest month of summer half of the year is
# less than 30 mm and less than one-third of the wettest month
# of the winter half"""
dmsp = min(m['summerppt'])
if (dmsp < 30 and dmsp < (max(m['winterppt'])/3)):
return 's'
# w
# Precipitation in driest month of the winter half of the year
# less than one-tenth of the amount in the wettest month of
# the summer half
elif min(m['winterppt']) < (max(m['summerppt'])/10):
return 'w'
# s and w failed to return anything
else:
return 'f'
def e_second(m, y):
# T
# Temperature of warmest month greater than 0 degrees Celsius
# but less than 10 degrees Celsius
if 0 < max(m['tave']) < 10:
return 'T'
# F
# Temperature of warmest month 0 degrees Celsius or below
elif max(['tave']) <= 0:
return 'F'
else:
return ''
def c_d_third(m, y):
"""returns third letter of the Koppen-Geiger classification
in the cases that the first letter is C or D"""
# d
# Temperature of coldest month less than –38 degrees Celsius
# (d designation then used instead of a, b, or c)
if min(m['tave']) < -38: # that's really unpleasantly cold
return 'd'
# a
# Temperature of warmest month 22 degrees Celsius or above
elif max(m['tave']) >= 22:
return 'a'
# b
# Temperature of each of four warmest months 10 degrees Celsius
# or above but warmest month less than 22 degrees Celsius
elif all([x >= 10 for x in sorted(m['tave'], reverse=True)[:4]]):
return 'b'
# c
# Temperature of one to three months 10 degrees Celsius or above
# but warmest month less than 22 degrees Celsius
elif max(m['tave']) >= 10:
return 'c'
return ''
Now that we have the helpers and the functions to return the three different letters, let's put it together.
We start by using our helper functions to grab 12-month series of temperature and precipitation data, as well as the yearly average temp and precip. Then we call the letter functions using the "monthlies" and "yearlies" as input.
def kg(zsv):
"""Classify a zone/subzone/variant to a Koppen-Geiger type.
Returns a tuple of:
The classification string, the monthly temperature and precip data,
and the yearly average temperature and precipitation."""
monthlies = {
'tave': [zsv[i] for i in twelvemonther('Tave')],
'summertave': [zsv[i] for i in summer('Tave')],
'wintertave': [zsv[i] for i in winter('Tave')],
'ppt': [zsv[i] for i in twelvemonther('PPT')],
'summerppt': [zsv[i] for i in summer('PPT')],
'winterppt': [zsv[i] for i in winter('PPT')],
}
# TODO: blank, fetch if needed
yearlies = {
#average annual temperature in deg C
't': sum(monthlies['tave']) / len(monthlies['tave']),
#average annual precipitation in mm
'r': sum(monthlies['ppt']) / len(monthlies['ppt']),
}
l1 = first(monthlies, yearlies)
if (l1 == 'C' or l1 == 'D'):
l2 = c_d_second(monthlies, yearlies)
elif l1 == 'E':
l2 = e_second(monthlies, yearlies)
else:
l2 = ''
l3 = c_d_third(monthlies, yearlies)
return (l1 + l2 + l3, monthlies, yearlies)
Ok, let's iterate through all of the filtered zone/subzone/variants and see what our function spits out. We'll call it c1990 for "classification 1990", but we'll also keep a list of the entire output of the classification function, which includes temperature and precipitation data, in another variable called allout1190. We'll print out some of the classification, but only the first 15 lines to avoid many pages of output.
allout1990 = [(row[1][1], kg(row[1])) for row in fdf.iterrows()]
c1990 = [[row[0], row[1][0]] for row in allout1990]
c1990[:15]
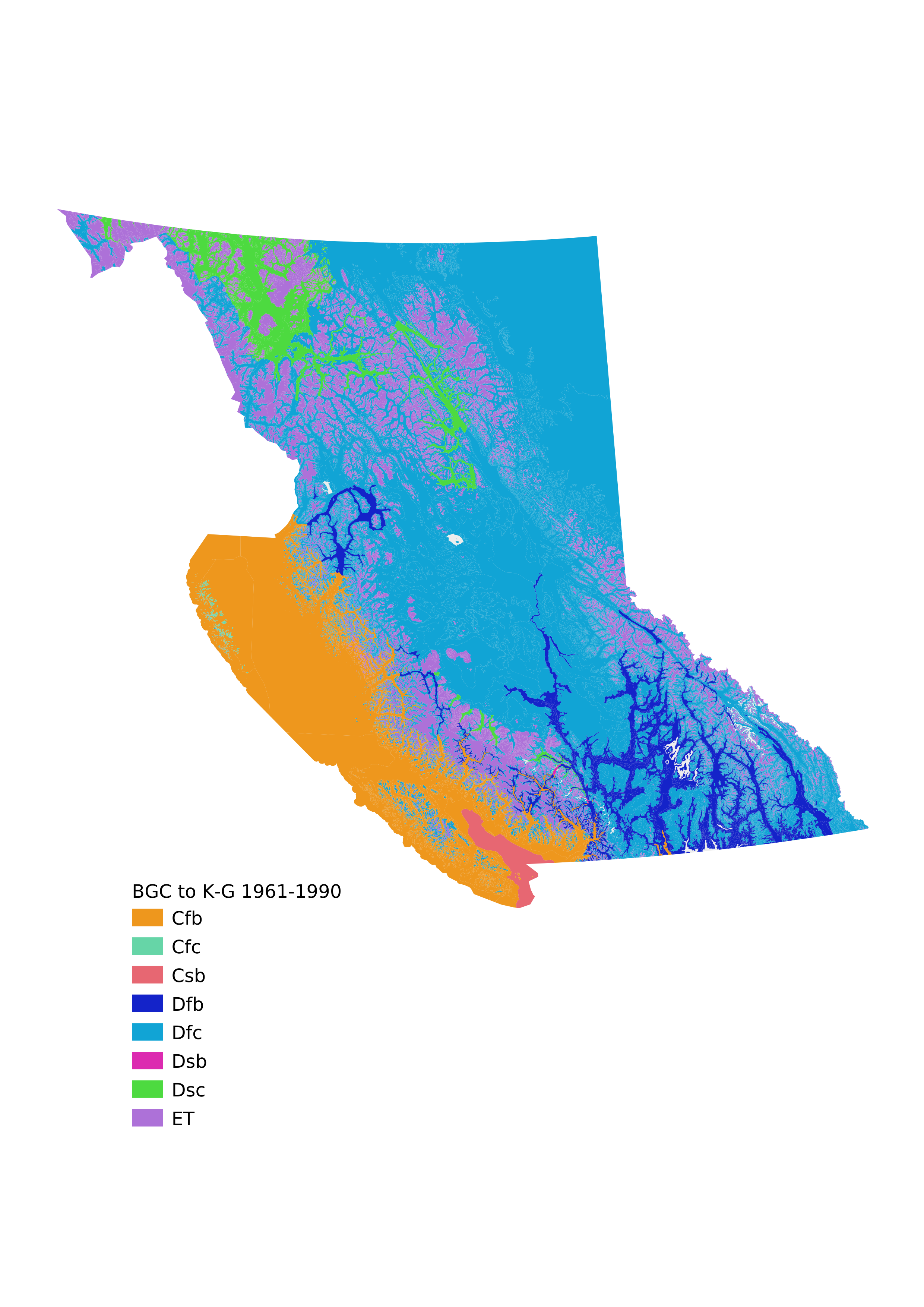
[['BAFAun', 'ET'], ['BAFAunp', 'ET'], ['BG xh 1', 'Cfb'], ['BG xh 2', 'Dfb'], ['BG xh 3', 'Dfb'], ['BG xw 1', 'Dfb'], ['BG xw 2', 'Dfb'], ['BWBSdk', 'Dsc'], ['BWBSmk', 'Dfc'], ['BWBSmw', 'Dfc'], ['BWBSvk', 'Dfc'], ['BWBSwk 1', 'Dfc'], ['BWBSwk 2', 'Dfc'], ['BWBSwk 3', 'Dfc'], ['CDF mm', 'Csb']]
Now we can add the Koppen-Geiger classification strings as attributes to a GIS file and create a categorized map.
We can compare that map to others generated on a global scale using the K-G categories; we would expect that they should roughly match, but the categorization generated from the BGC data should be much higher resolution and more accurate as it's derived from much more detailed data than the global dataset could possibly be.
First let's export a Comma Separated Values file (.csv) with the BGC labels in one column and the K-G classifications in the other.
import csv
with open('bec_2_k-g_1961-1990.csv','w') as f:
w = csv.writer(f)
# header row
w.writerow(['BGC', 'KG'])
# data rows
for row in c1990:
w.writerow(row)
Now we cheat, and load that CSV file into QGIS along with the BEC_BIOGEOCLIMATIC_POLY file from the BC government GIS portal (it would be better to do the mapping right here in the Jupyter notebook to make the whole project more self-contained, but it's faster to start using QGIS).
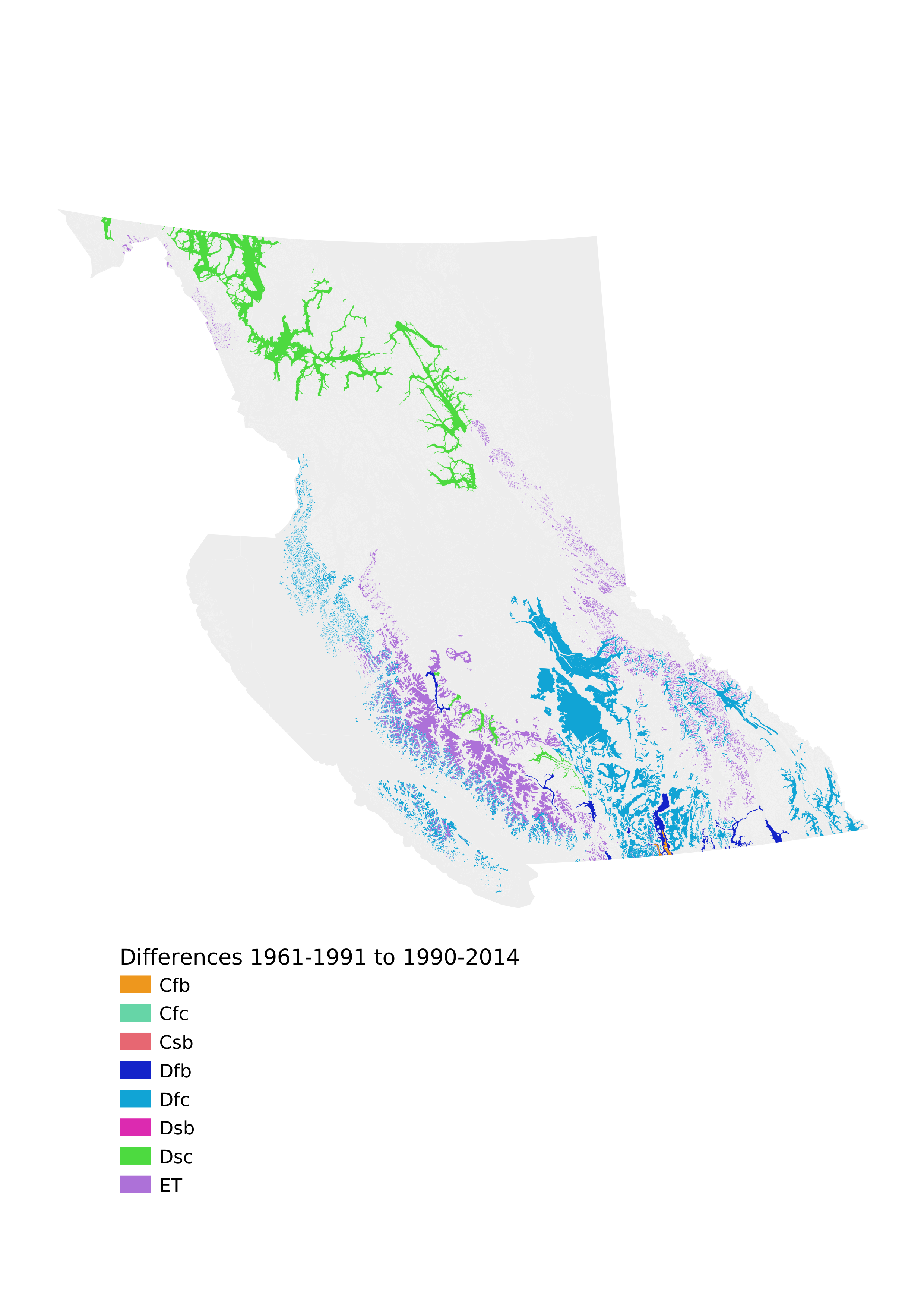
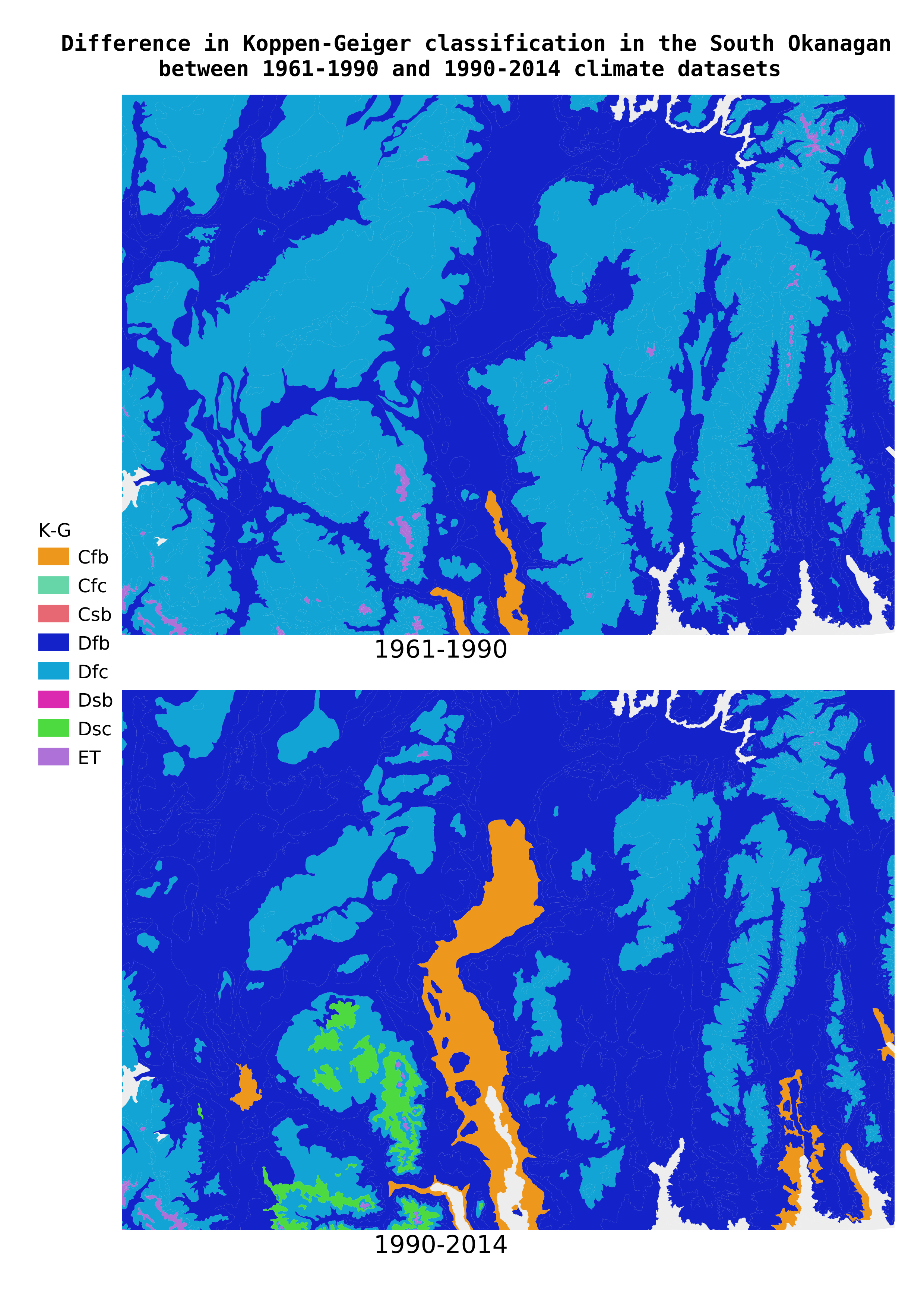
The next two pages are maps exported from QGIS with the Koppen-Geiger classifications color-coded (randomly; we should probably try to match the colors to some global K-G maps, but for now we just want to see the results to check if they make sense at first blush).

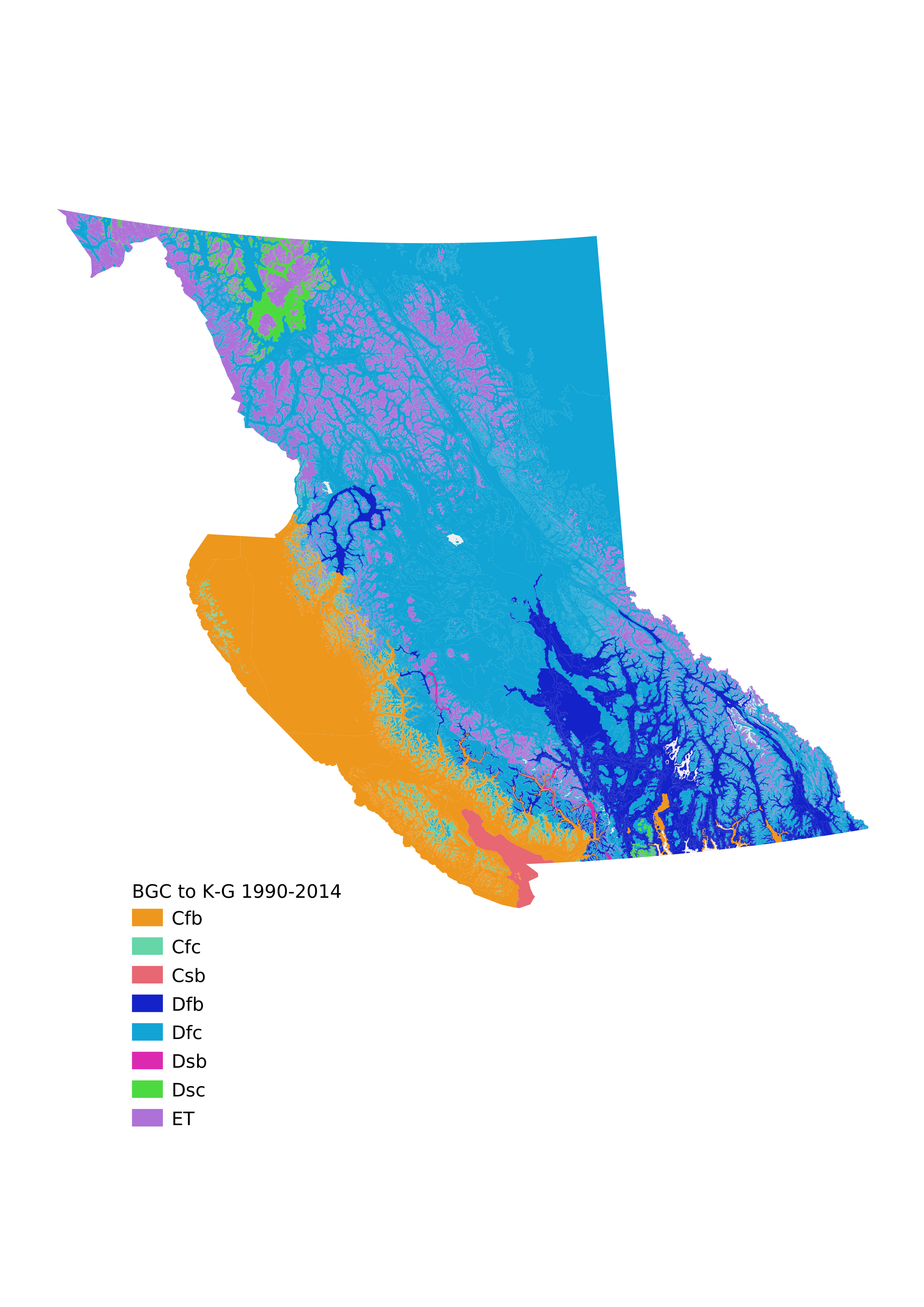
Now that we've built all of the scaffolding to classify BGC zone/subzone/variants by Koppen-Geiger, we can experiment easily. What would happen if we used the most recent data from ClimateBC, the series from 1990-2014? Let's find out.
# Filter the original DataFrame for 1990-2014
fdf2014 = df[(df['period']=='1990-2014') & (df['Var']=='mean')]
fdf2014
| ID | BGC | period | Var | Tmax01 | Tmax02 | Tmax03 | Tmax04 | Tmax05 | Tmax06 | ... | bFFP | eFFP | FFP | PAS | EMT | EXT | Eref | CMD | MAR | RH | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 52 | 53 | BAFAun | 1990-2014 | mean | -7.36 | -5.52 | -4.26 | 1.09 | 6.40 | 10.34 | ... | 181.45 | 232.76 | 51.31 | 976.48 | -44.43 | 24.31 | 265.54 | 27.69 | -1590.05 | 67.52 |
| 108 | 109 | BAFAunp | 1990-2014 | mean | -3.40 | -1.54 | 0.47 | 3.97 | 8.69 | 11.94 | ... | 180.46 | 241.06 | 60.59 | 1003.45 | -41.48 | 27.29 | 367.60 | 97.56 | -1588.93 | 63.66 |
| 164 | 165 | BG xh 1 | 1990-2014 | mean | 1.21 | 4.56 | 10.74 | 16.16 | 21.27 | 24.67 | ... | 108.32 | 291.53 | 183.20 | 36.61 | -29.82 | 39.23 | 802.90 | 589.73 | -1618.65 | 66.10 |
| 220 | 221 | BG xh 2 | 1990-2014 | mean | -0.25 | 3.41 | 9.66 | 15.49 | 20.49 | 24.09 | ... | 119.11 | 281.01 | 161.89 | 52.15 | -33.37 | 37.53 | 758.01 | 555.76 | -1590.45 | 63.09 |
| 276 | 277 | BG xh 3 | 1990-2014 | mean | -1.14 | 2.99 | 9.07 | 15.03 | 20.00 | 23.64 | ... | 128.68 | 274.69 | 146.01 | 63.05 | -34.92 | 37.26 | 738.72 | 516.09 | -1590.48 | 61.23 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 11644 | 11645 | SWB mks | 1990-2014 | mean | -7.38 | -4.60 | -3.17 | 3.46 | 8.74 | 12.79 | ... | 180.82 | 237.91 | 57.09 | 480.05 | -44.37 | 26.15 | 315.03 | 39.68 | -1590.60 | 65.62 |
| 11700 | 11701 | SWB un | 1990-2014 | mean | -9.26 | -5.37 | -2.05 | 4.75 | 10.50 | 15.20 | ... | 173.31 | 240.92 | 67.63 | 367.05 | -45.50 | 28.35 | 352.19 | 108.58 | -1591.23 | 62.28 |
| 11756 | 11757 | SWB uns | 1990-2014 | mean | -8.45 | -5.29 | -3.09 | 3.21 | 9.03 | 13.57 | ... | 175.76 | 237.59 | 61.82 | 446.18 | -45.51 | 26.83 | 312.43 | 73.35 | -1591.08 | 63.36 |
| 11812 | 11813 | SWB vk | 1990-2014 | mean | -5.07 | -2.70 | -0.12 | 5.53 | 10.74 | 14.21 | ... | 157.79 | 256.35 | 98.57 | 1327.76 | -37.62 | 27.25 | 341.46 | 14.71 | -1675.32 | 73.08 |
| 11868 | 11869 | SWB vks | 1990-2014 | mean | -6.76 | -4.31 | -1.81 | 4.01 | 9.29 | 12.85 | ... | 171.90 | 246.25 | 74.34 | 2203.05 | -40.00 | 26.15 | 311.08 | 7.80 | -1590.87 | 71.58 |
212 rows × 251 columns
Same number of rows. Good news there; we don't want to be classifying zones by an incomplete set of climate numbers.
Ok, let's run this series through our classification function. Any differences? Let's create a comparison and look at them side-by-side (again only 15 lines).
allout2014 = [(row[1][1], kg(row[1])) for row in fdf2014.iterrows()]
# N.B. this zip is risky; if the datasets are not identically
# ordered something bad will happen. Should improve this with
# a dictionary lookup instead of 2-list zip. For now it works,
# as long as we check that BGC labels are the same in each row.
c2014 = [[row[0], row[1][0]] for row in allout2014]
comp = [row for row in zip(c1990, c2014)]
comp[:15]
[(['BAFAun', 'ET'], ['BAFAun', 'ET']), (['BAFAunp', 'ET'], ['BAFAunp', 'ET']), (['BG xh 1', 'Cfb'], ['BG xh 1', 'Cfa']), (['BG xh 2', 'Dfb'], ['BG xh 2', 'Dfb']), (['BG xh 3', 'Dfb'], ['BG xh 3', 'Dfb']), (['BG xw 1', 'Dfb'], ['BG xw 1', 'Dfb']), (['BG xw 2', 'Dfb'], ['BG xw 2', 'Dfb']), (['BWBSdk', 'Dsc'], ['BWBSdk', 'Dfc']), (['BWBSmk', 'Dfc'], ['BWBSmk', 'Dfc']), (['BWBSmw', 'Dfc'], ['BWBSmw', 'Dfc']), (['BWBSvk', 'Dfc'], ['BWBSvk', 'Dfc']), (['BWBSwk 1', 'Dfc'], ['BWBSwk 1', 'Dfc']), (['BWBSwk 2', 'Dfc'], ['BWBSwk 2', 'Dfc']), (['BWBSwk 3', 'Dfc'], ['BWBSwk 3', 'Dfc']), (['CDF mm', 'Csb'], ['CDF mm', 'Csb'])]
Yes, there are a few differences! Let's isolate and count them.
diff1990_2014 = [(row[0][0], row[0][1], row[1][1])
for row in comp if (row[0] != row[1])]
for row in diff1990_2014:
print(row)
print(f'\nThere are {len(diff1990_2014)} zone/subzone/variants '\
'that change Koppen-Geiger classification when using the '\
'1990-2014 data instead of the 1961-1990 data')
('BG xh 1', 'Cfb', 'Cfa')
('BWBSdk', 'Dsc', 'Dfc')
('CMA unp', 'ET', 'Dfc')
('ESSFdcp', 'ET', 'Dfc')
('ESSFdh 1', 'Dfc', 'Dfb')
('ESSFdh 2', 'Dfc', 'Dfb')
('ESSFmh', 'Dfc', 'Dfb')
('ESSFmkp', 'ET', 'Dfc')
('ESSFvcp', 'ET', 'Dfc')
('ESSFwcp', 'ET', 'Dfc')
('ESSFxc 1', 'Dfc', 'Dsc')
('ESSFxcw', 'ET', 'Dfc')
('ESSFxv 1', 'ET', 'Dfc')
('ESSFxv 2', 'ET', 'Dfc')
('ICH dk', 'Dfc', 'Dfb')
('ICH mk 2', 'Dfc', 'Dfb')
('ICH mk 3', 'Dfc', 'Dfb')
('ICH mk 4', 'Dfc', 'Dfb')
('ICH mk 5', 'Dfc', 'Dfb')
('ICH mw 1', 'Dfc', 'Dfb')
('ICH vk 1', 'Dfc', 'Dfb')
('ICH wk 2', 'Dfc', 'Dfb')
('ICH xw', 'Dfb', 'Cfb')
('IDF dc', 'Dsc', 'Dfb')
('IDF dk 1', 'Dfc', 'Dfb')
('IDF dk 3', 'Dfc', 'Dfb')
('IDF dw', 'Dsc', 'Dfc')
('IDF ww', 'Dfb', 'Dsb')
('MH mm 1', 'Dfc', 'Cfc')
('MH unp', 'ET', 'Dfc')
('MH wh 1', 'Dfc', 'Cfb')
('MS dm 1', 'Dfc', 'Dfb')
('MS dm 2', 'Dfc', 'Dfb')
('MS dw', 'Dfc', 'Dfb')
('PP xh 1', 'Dfb', 'Cfb')
('PP xw', 'Dsb', 'Cfb')
('SBS dw 1', 'Dfc', 'Dfb')
('SBS mw', 'Dfc', 'Dfb')
There are 38 zone/subzone/variants that change Koppen-Geiger classification when using the 1990-2014 data instead of the 1961-1990 data
And map the 1990-2014 data, as well as the differences.
# Create a CSV of the 1990-2014 classification
with open('bec_2_k-g_1990_2014.csv','w') as f:
w = csv.writer(f)
# header row
w.writerow(['BGC', 'KG'])
# data rows
for row in c2014:
w.writerow(row)
# Create a CSV of the differences between 1961-1990 and 1990-2014
with open('bec_2_k-g_differences_1961-1990_1990-2014.csv','w') as f:
w = csv.writer(f)
# header row
w.writerow(['BGC', 'KG1960-1992', 'KG1990-2014'])
# data rows
for row in diff1990_2014:
w.writerow(row)
details = [[row[0], row[1][0], row[1][1]['tave'], row[1][1]['ppt']] for row in allout2014]
with open('bec_2_k-g_1990_2014_with_temp_and_precip.csv','w') as f:
w = csv.writer(f)
# header row
w.writerow(['BGC', 'KG', 'Tave', 'PPT'])
# data rows
for row in details:
w.writerow(row)
details = [[row[0], row[1][0], row[1][1]['tave'], row[1][1]['ppt']] for row in allout1990]
with open('bec_2_k-g_1961-1990_with_temp_and_precip.csv','w') as f:
w = csv.writer(f)
# header row
w.writerow(['BGC', 'KG', 'Tave', 'PPT'])
# data rows
for row in details:
w.writerow(row)
Now let's map those!